- Home
- /
- News
- /
- Industry News
How to calculate required input power for a gearmotor

The first place to start when sizing a gearmotor is to determine the required output torque and speed.
But once torque and speed are defined, you’ll also want to know the required input power for the motor — particularly if the gearmotor uses an AC induction motor, where the power rating (typically given in horsepower) is used as a key factor in sizing.
Relationship between work and power
Before we look at how to calculate power, let’s review the relationship between power and work.
Work is defined as force applied over a distance:

W = work (J)
F = force (N)
d = distance, or displacement (m)
Mechanical power is the time rate at which work is done, so work divided by time:
P = mechanical power (watt)
W = work (J)
t = time (s)
Mechanical power can also be written as:

Note that distance divided by time (d/t) is velocity, so power can be written as force times velocity:
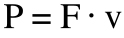
v = velocity (m/s)
Power equations for electric motors: metric units
Electric motors produce torque (rather than force) through rotational motion (rather than linear distance), so power is equal to torque multiplied by angular velocity:
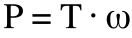
P = mechanical power (W)
T = torque (Nm)
ω = angular velocity (rad/s)
Note that angular velocity has units of radians per second. If speed is given in rotations per minute (rot/min or rpm), be sure to convert rotations per minute to radians per second:
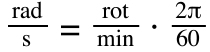
Converting from Watts to horsepower
Although the SI unit of power is the watt, in discussions of motor power, the Imperial unit of horsepower is often used.
In the 1780s, James Watt and Matthew Boulton defined 1 horsepower (hp) as 33,000 ft-lb/min, which, is 44,742 Nm/min.

Converting this from Nm/min to Nm/s gives us 746 Nm/s, or 746 Watts. Therefore, to convert power from watts to horsepower, divide the power in watts by 746.

In gearmotor applications, torque and speed are still often given in Imperial units. In these cases, horsepower can be calculated directly, with the use of a conversion factor:
When torque is given in lb-ft and speed in rpm:
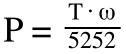
P = mechanical power (hp)
T = torque (lb-ft)
ω = angular velocity (rpm)
5252 = 33,0000 ft-lb/min ÷ 2π rad/rot
When torque is given in lb-in and speed in rpm:

P = mechanical power (hp)
T = torque (lb-in)
ω = angular velocity (rpm)
63,025 = 33,000 ft-lb/min * 12 in/ft ÷ 2π rad/rot
Input power for gearmotors
Each equation for mechanical power given above can apply when sizing a gearmotor, depending on what units of torque and speed are being used.
However, when determining the input power required for the motor, the efficiency of the gearmotor assembly at transmitting that power to the load must be taken into account. Therefore, regardless of which equation above is used to calculate the required output power, the required input power at the motor is calculated as:
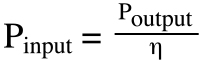
η = gearmotor efficiency
Note that efficiency can vary greatly, depending on the motor, type of gearing used, and the gear ratio. For example, gearmotors that use hypoid gearing can have efficiencies of greater than 90 percent, while those that use worm gears can have efficiencies ranging from less than 40 percent up to about 80 percent.
Relationship between work and power
Before we look at how to calculate power, let’s review the relationship between power and work.
Work is defined as force applied over a distance:
W = work (J)
F = force (N)
d = distance, or displacement (m)
Mechanical power is the time rate at which work is done, so work divided by time:
P = mechanical power (watt)
W = work (J)
t = time (s)
Mechanical power can also be written as:

Note that distance divided by time (d/t) is velocity, so power can be written as force times velocity:
v = velocity (m/s)
Power equations for electric motors: metric units
Electric motors produce torque (rather than force) through rotational motion (rather than linear distance), so power is equal to torque multiplied by angular velocity:
P = mechanical power (W)
T = torque (Nm)
ω = angular velocity (rad/s)
Note that angular velocity has units of radians per second. If speed is given in rotations per minute (rot/min or rpm), be sure to convert rotations per minute to radians per second:
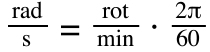
Converting from Watts to horsepower
Although the SI unit of power is the watt, in discussions of motor power, the Imperial unit of horsepower is often used.
In the 1780s, James Watt and Matthew Boulton defined 1 horsepower (hp) as 33,000 ft-lb/min, which, is 44,742 Nm/min.

Converting this from Nm/min to Nm/s gives us 746 Nm/s, or 746 Watts. Therefore, to convert power from watts to horsepower, divide the power in watts by 746.

In gearmotor applications, torque and speed are still often given in Imperial units. In these cases, horsepower can be calculated directly, with the use of a conversion factor:
When torque is given in lb-ft and speed in rpm:
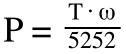
P = mechanical power (hp)
T = torque (lb-ft)
ω = angular velocity (rpm)
5252 = 33,0000 ft-lb/min ÷ 2π rad/rot
When torque is given in lb-in and speed in rpm:

P = mechanical power (hp)
T = torque (lb-in)
ω = angular velocity (rpm)
63,025 = 33,000 ft-lb/min * 12 in/ft ÷ 2π rad/rot
Input power for gearmotors
Each equation for mechanical power given above can apply when sizing a gearmotor, depending on what units of torque and speed are being used.
However, when determining the input power required for the motor, the efficiency of the gearmotor assembly at transmitting that power to the load must be taken into account. Therefore, regardless of which equation above is used to calculate the required output power, the required input power at the motor is calculated as:
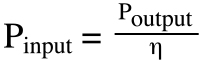
η = gearmotor efficiency
Note that efficiency can vary greatly, depending on the motor, type of gearing used, and the gear ratio. For example, gearmotors that use hypoid gearing can have efficiencies of greater than 90 percent, while those that use worm gears can have efficiencies ranging from less than 40 percent up to about 80 percent.
Key: Vertical 3 Phase ac induction motors, electric motor, Vertical Inverter Duty motor, DC Brake motor Oil Pressure Motor, helical gear motor, AC mini Induction DC gear motor, Gear reducer motor series, NMRV NRV worm reducer series, Worm reducer series, Horizontal Inverter duty, worm gear series, ac motor, vertical gearmotor, helical horizontal gearmotor, gear reduce motor, bevel gearmotor, cyclo gear motor, NMRV gear motor, worm reducer
Newer articles
- Stepper Motors in Precision Motion Control and Positioning (14/11/2020)
- The Differences Between Spur And Planetary Gear Motors (16/11/2020)
- 5 Layout Ideas For Gear Motor Applications (17/11/2020)
- Top Benefits of Using Geared Motors (17/11/2020)
- Gear Motors in Precision Motion Applications (13/11/2020)
- What is linear motion design engineering? (12/11/2020)
- What are gearmotors and what do they do? (09/11/2020)
- What is pole count and why does it matter? (10/11/2020)
- How to select and specify stepper motors (11/11/2020)
- How to Select a Gearmotor in Four Simple Steps (07/11/2020)
Older articles
- Difference Between AC and DC Motor (05/11/2020)
- Which types of DC motors can be used as servo motors? (03/11/2020)
- What are multi-stage gearboxes and when are they used? (02/11/2020)
- What are electromagnetic power-off brakes and where are they used? (01/11/2020)
- What are double- and triple-stack hybrid stepper motors ? (30/10/2020)
- What are different ways to express a gear ratio? (29/10/2020)
- What are the performance benefits of 5-phase stepper motors? (28/10/2020)
- Single-phase, two-phase and three-phase motors: all you need to know (28/10/2020)
- How Does A Brushless Electric Motor Work? (20/10/2020)
- Steps to calculate a gear ratio (26/10/2020)





Join